Unique factorization domain

In mathematics, a unique factorization domain (UFD) is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements (or irreducible elements), analogous to the fundamental theorem of arithmetic for the integers. UFDs are sometimes called factorial rings, following the terminology of Bourbaki.

Note that unique factorization domains appear in the following chain of class inclusions:

Commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields

1 Definition
2 Examples
3 Non-examples
4 Properties
5 Equivalent conditions for a ring to be a UFD
6 References

Definition

Formally, a unique factorization domain is defined to be an integral domain R in which every non-zero x of R can be written as a product (including an empty product) of irreducible elements p_i of R and a unit u:

x = u p₁ p₂ ... p_n with n≥0

and this representation is unique in the following sense: If q₁,...,q_m are irreducible elements of R and w is a unit such that

x = w q₁ q₂ ... q_m with m≥0,

then m = n and there exists a bijective map φ : {1,...,n} -> {1,...,m} such that p_i is associated to q_φ(i) for i ∈ {1, ..., n}.

The uniqueness part is usually hard to verify, which is why the following equivalent definition is useful:

A unique factorization domain is an integral domain R in which every non-zero element can be written as a product of a unit and prime elements of R.

Examples

Most rings familiar from elementary mathematics are UFDs:

All principal ideal domains, hence all Euclidean domains, are UFDs. In particular, the integers (also see fundamental theorem of arithmetic), the Gaussian integers and the Eisenstein integers are UFDs.
Any field is trivially a UFD, since every non-zero element is a unit. Examples of fields include rational numbers, real numbers, and complex numbers.
If R is a UFD, then so is R[X], the ring of polynomials with coefficients in R. Unless R is a field, R[X] is not a principal ideal domain. By iteration, a polynomial ring in any number of variables over any UFD (and in particular over a field) is an UFD.
The Auslander–Buchsbaum theorem states that every regular local ring is a UFD.

Further examples of UFDs are:

The formal power series ring K[[X₁,...,X_n]] over a field K (or more generally over a PID but not over a UFD).

Non-examples

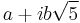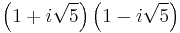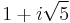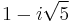The quadratic integer ring $\mathbb Z[\sqrt{-5}]$ of all complex numbers of the form $a%2Bib\sqrt{5}$ , where a and b are integers. Then 6 factors as both (2)(3) and as $\left(1%2Bi\sqrt{5}\right)\left(1-i\sqrt{5}\right)$ . These truly are different factorizations, because the only units in this ring are 1 and −1; thus, none of 2, 3, $1%2Bi\sqrt{5}$ , and $1-i\sqrt{5}$ are associate. It is not hard to show that all four factors are irreducible as well, though this may not be obvious. See also algebraic integer.

Most factor rings of a polynomial ring are not UFDs. Here are two examples:

Let $R$ be any commutative ring. Then $R[X,Y,Z,W]/(XY-ZW)$ is not a UFD. The proof is in two parts.

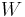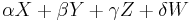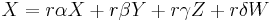First we must show $X$ , $Y$ , $Z$ , and $W$ are all irreducible. Grade $R[X,Y,Z,W]/(XY-ZW)$ by degree. Assume for a contradiction that $X$ has a factorization into two non-zero non-units. Since it is degree one, the two factors must be a degree one element $\alpha X %2B \beta Y %2B \gamma Z %2B \delta W$ and a degree zero element $r$ . This gives $X = r\alpha X %2B r\beta Y %2B r\gamma Z %2B r\delta W$ . 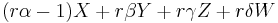In $R[X,Y,Z,W]$ , then, the degree one element $(r\alpha-1) X %2B r\beta Y %2B r\gamma Z %2B r\delta W$ must be an element of the ideal $(XY-ZW)$ , but the non-zero elements of that ideal are degree two and higher. 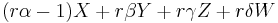Consequently, $(r\alpha-1) X %2B r\beta Y %2B r\gamma Z %2B r\delta W$ must be zero in $R[X,Y,Z,W]$ . 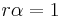That implies that $r\alpha = 1$ , so $r$ is a unit, which is a contradiction. 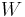$Y$ , $Z$ , and $W$ are irreducible by the same argument.

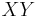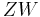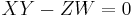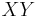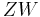Next, the element $XY$ equals the element $ZW$ because of the relation $XY - ZW = 0$ . That means that $XY$ and $ZW$ are two different factorizations of the same element into irreducibles, so $R[X,Y,Z,W]/(XY-ZW)$ is not a UFD.

The ring of holomorphic functions in a single complex variable is not a UFD, since there exist holomorphic functions with an infinity of zeros, and thus an infinity of irreducible factors, while a UFD factorization must be finite, e.g.:

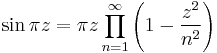$\sin \pi z = \pi z \prod_{n=1}^{\infty} \left(1-{{z^2}\over{n^2}}\right)$ .

A Noetherian domain is not necessarily a UFD. Although any non-zero non-unit in a Noetherian domain is the product of irreducible elements, this product is not necessarily unique.

Properties

Some concepts defined for integers can be generalized to UFDs:

In UFDs, every irreducible element is prime. (In any integral domain, every prime element is irreducible, but the converse does not always hold.) Note that this has a partial converse: any Noetherian domain is a UFD if every irreducible element is prime.

Any two (or finitely many) elements of a UFD have a greatest common divisor and a least common multiple. Here, a greatest common divisor of a and b is an element d which divides both a and b, and such that every other common divisor of a and b divides d. All greatest common divisors of a and b are associated.

Any UFD is integrally closed. In other words, if R is an integral domain with quotient field K, and if an element k in K is a root of a monic polynomial with coefficients in R, then k is an element of R.

Equivalent conditions for a ring to be a UFD

A Noetherian integral domain is a UFD if and only if every height 1 prime ideal is principal. Also, a Dedekind domain is a UFD if and only if its ideal class group is trivial. In this case it is in fact a principal ideal domain.

There are also equivalent conditions for non-noetherian integral domains. Let A be an integral domain. Then the following are equivalent.

A is a UFD.
Every nonzero prime ideal of A contains a prime element. (Kaplansky)
A satisfies ascending chain condition on principal ideals (ACCP), and the localization S⁻¹A is a UFD, where S is a multiplicatively closed subset of A generated by prime elements. (Nagata criterion)
A satisfies (ACCP) and every irreducible is prime.
A is a GCD domain (i.e., any two elements have a greatest common divisor) satisfying (ACCP).
A is a Schreier domain,^[1] and every nonzero nonunit can be expressed as a finite product of irreducible elements (that is, A is atomic.)
A has a divisor theory in which every divisor is principal.

In practice, (2) and (3) are the most useful conditions to check. For example, it follows immediately from (2) that a PID is a UFD, since, in a PID, every prime ideal is generated by a prime element.

References

^ A Schreier domain is an integrally closed integral domain where, whenever x divides yz, x can be written as x = x₁ x₂ so that x₁ divides y and x₂ divides z. In particular, a GCD domain is a Schreier domain

B. Hartley; T.O. Hawkes (1970). Rings, modules and linear algebra. Chapman and Hall. ISBN 0-412-09810-5. Chap. 4.
Chapter II.5 of Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0
David Sharpe (1987). Rings and factorization. Cambridge University Press. ISBN 0-521-33718-6.
Samuel, Pierre (1968). "Unique factorization". The American Mathematical Monthly (75): 945–952. ISSN 0002-9890